
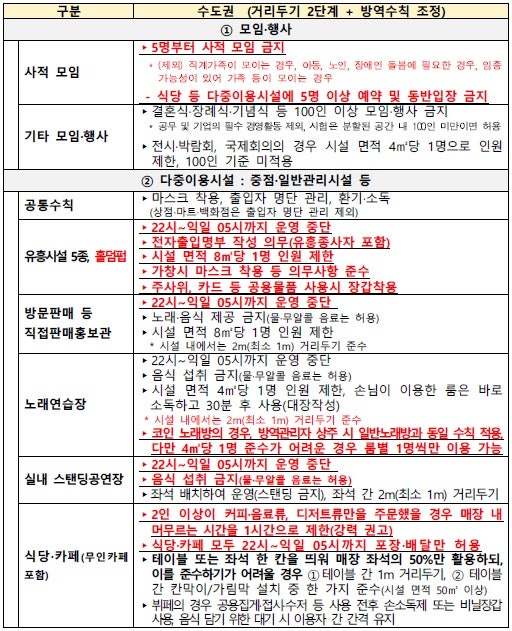
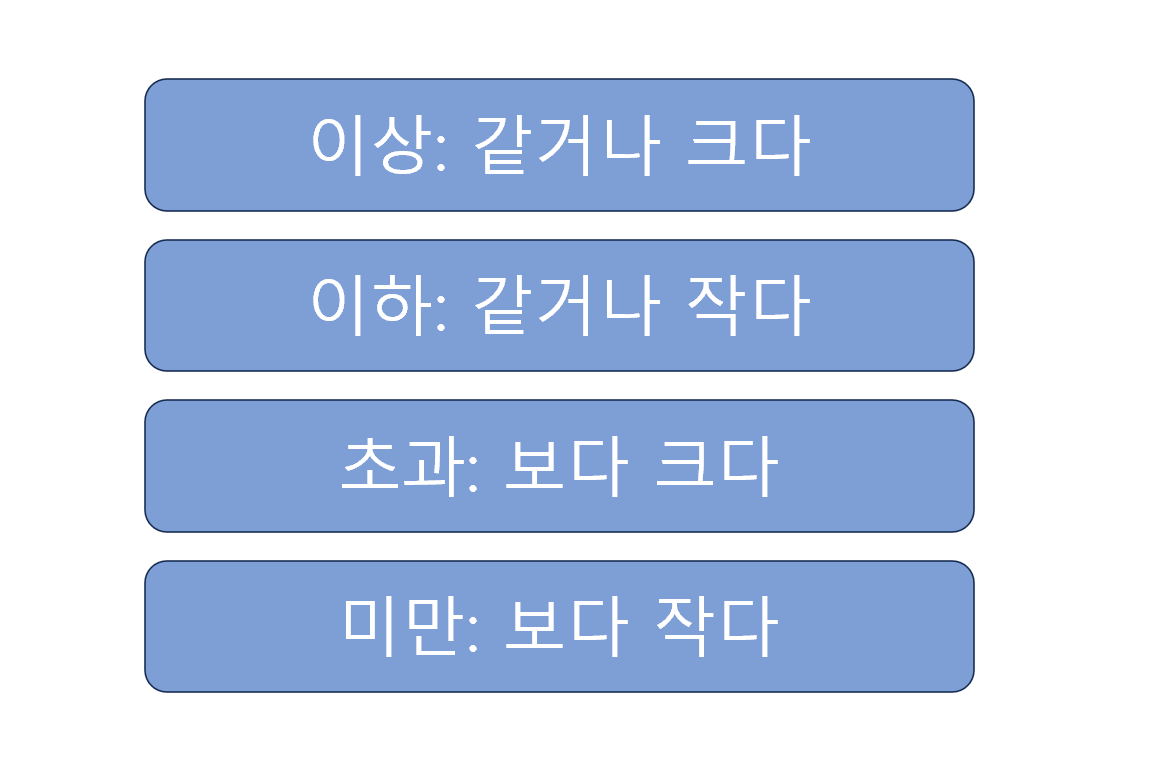
이상과 이하의 개념은 수학적, 논리적 상황에서 빈번하게 사용되며, 많은 사람들에게 혼란을 줄 수 있는 주제 중 하나입니다. 이 두 용어는 특정 조건이나 범위에 대한 이해를 돕기 위해 사용되는데, 올바른 사용을 통해 여러 문제를 해결하고 정확한 결정을 내리는 데 기여할 수 있습니다. 따라서, 이 블로그 글에서는 이상과 이하의 차이점과 사용 방법, 그리고 이들을 올바르게 이해하고 활용하는 방법에 대해 깊이 있게 살펴보겠습니다.
이상과 이하의 정의와 개념



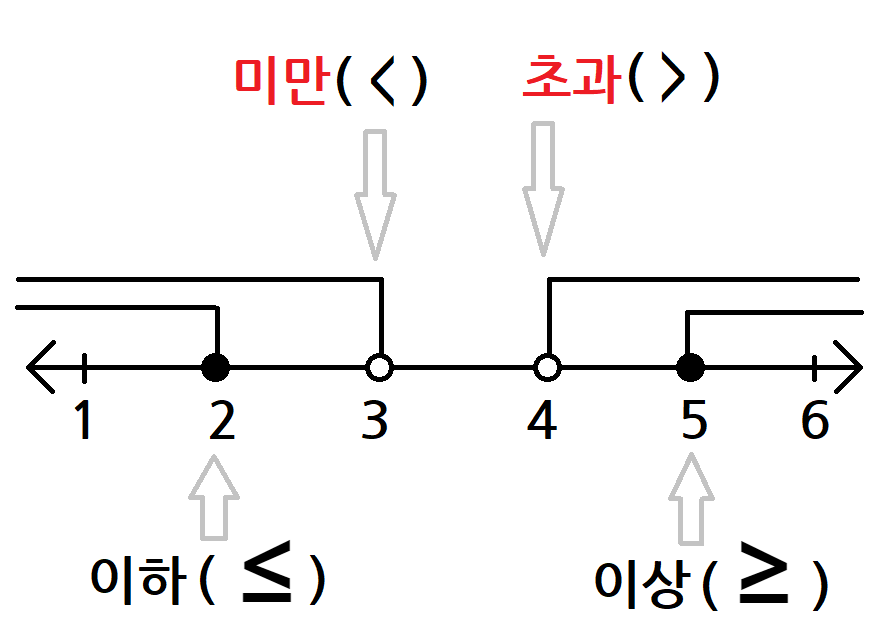
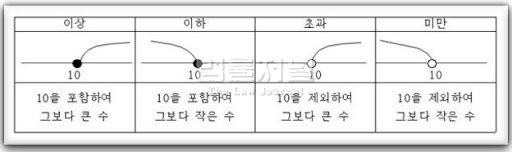
먼저 이상(≥)과 이하(≤)의 개념을 명확히 이해하는 것이 중요합니다. 두 용어는 주로 부등식을 사용하여 수학적 표현을 할 때 나타납니다. 이상은 특정 값보다 크거나 같은 것을 의미하며, 이하 역시 특정 값보다 작거나 같은 상황을 나타냅니다. 이러한 정의는 수학의 다양한 분야에서 적용될 수 있으며, 특히 통계학, 경제학, 물리학 등에서 널리 사용됩니다.
이상의 정의



이상의 개념을 깊이 있게 이해하기 위해서는 몇 가지 예를 살펴볼 필요가 있습니다. 예를 들어, "x ≥ 5"라는 표현은 x의 값이 5이상임을 의미합니다. 즉, x는 5, 6, 7, ...과 같은 값을 가질 수 있습니다. 이처럼 이상은 기준값과 같거나 그보다 큰 수치를 포함합니다. 따라서 이상은 우리가 주어진 범위 안에서 가능한 값들의 집합을 확대하는 역할을 합니다.
- 수학적 표현: x ≥ a
- 비교: x는 a보다 크거나 같다
- 사용 예: "이상한 사람"처럼 비유적으로 쓸 수도 있다.
이하의 정의



이제 이하에 대해 살펴보겠습니다. 이하(≤)는 보다 간단한 개념으로, 특정 값보다 작거나 같은 경우를 말합니다. 예를 들어, "y ≤ 10"이라는 표현은 y의 값이 10이하임을 의미하며, y는 10, 9, 8, ...과 같은 값을 가질 수 있습니다. 이처럼 이하 또한 주어진 기준 값보다 작거나 같은 수치를 포함하여, 가능한 값의 범위를 설정합니다.
- 수학적 표현: y ≤ b
- 비교: y는 b보다 작거나 같다
- 실제 예: "그것이 이하로 떨어졌다"처럼 실제 상황에서도 사용된다.
이상과 이하의 활용 사례

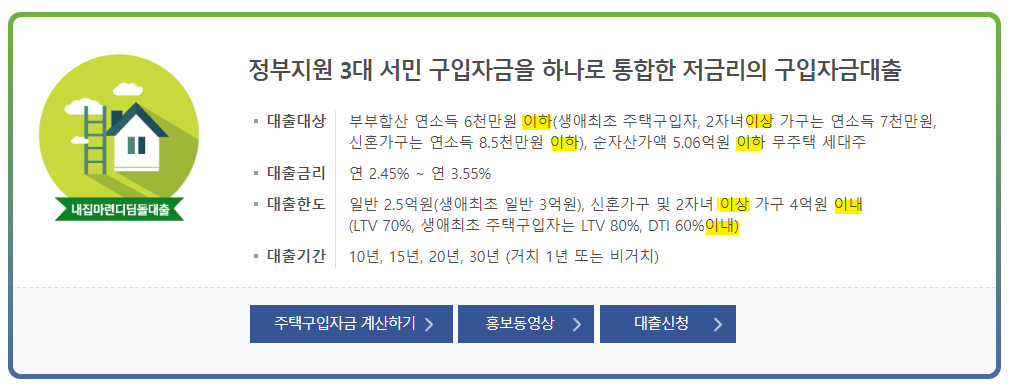
이상의 경우와 이하의 경우를 이해한 후에는 실제 활용 사례를 통해 그 중요성을 다시 한 번 살펴보겠습니다. 수학적 문제 해결뿐만 아니라 일상생활에서도 이들 용어는 자주 등장합니다.
수학적 문제 해결에서의 이상과 이하
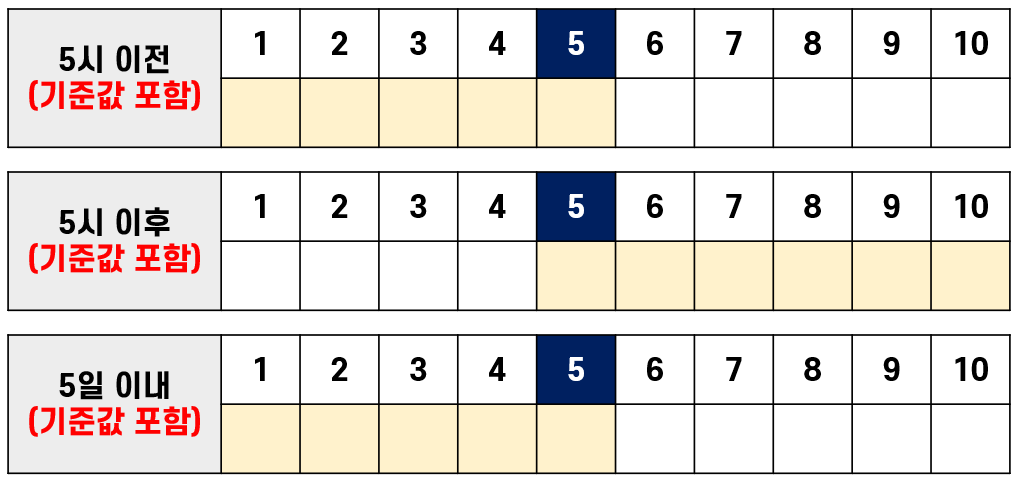
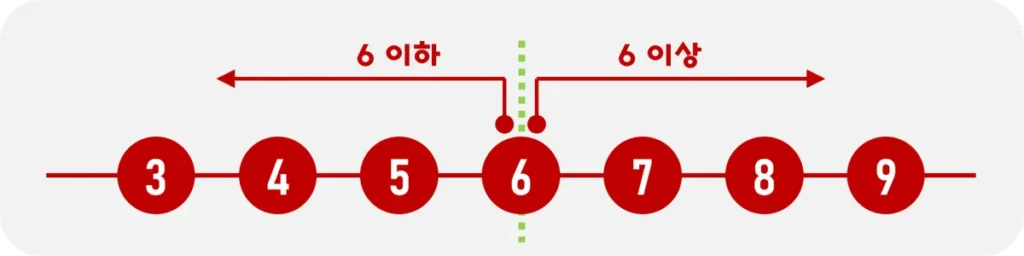
수학에서의 응용을 이해하기 위해, 간단한 예제를 통해 이상과 이하의 적용을 보여드리겠습니다. 예를 들어, 다음과 같은 문제를 생각해봅시다. "y는 10이하이며, 5이상의 값을 가진다." 이러한 표현은 다음과 같은 부등식으로 나타낼 수 있습니다: 5 ≤ y ≤ 10. 이 문제는 y의 값이 5와 10 사이에 위치해야 함을 명확히 보여줍니다. 이러한 수학적 표현은 주어진 조건을 명확히 파악하고 문제를 해결하는 데 필수적입니다.
일상생활에서의 이상과 이하

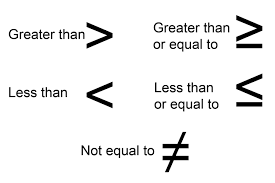

일상생활에서도 이상과 이하의 개념은 매우 중요합니다. 쇼핑을 할 때 우리가 할인된 가격을 찾을 때, "30% 이상 할인된 상품"이나 "50,000원 이하의 상품" 같은 표현을 사용합니다. 이러한 사용은 소비자에게 명확한 정보를 제공하고, 쉽게 결정하는 데 도움을 줍니다. 이처럼 비즈니스, 경제, 그리고 다양한 사회적 상황에서 이상과 이하의 이해는 매우 유용합니다.
사회적 의미


또한 이상의 경우와 이하의 경우는 사회적 맥락에서도 다양하게 적용될 수 있습니다. 예를 들어, "소득이 3,000만 원 이상"이라는 기준은 일정 수준 이상의 소득을 의미하며, 이는 정책적 결정이나 사회적 논의에서 중요한 기준이 됩니다. 반면에 "취업률이 70% 이하"라는 표현은 특정 경제적 상황을 나타내며, 이는 정책 입안 시 고려해야 할 중요한 요소 중 하나입니다.
결론 및 요약



이상과 이하의 차이를 이해하는 것은 많은 이들에게 중요한 통찰을 제공합니다. 이 두 개념은 단순히 수학적 표현에 국한되지 않고, 우리의 일상과 여러 사회적 상황에서도 밀접하게 연결되어 있습니다. 그러므로 이러한 개념을 올바르게 이해하고 사용함으로써 보다 나은 의사소통을 할 수 있으며, 다양한 문제를 해결하는 데 큰 도움이 될 것입니다.
결국, 이상은 특정 수치 이상의 값들을 포함하는 반면, 이하는 특정 수치 이하의 값들을 포함한다는 점이 가장 큰 차이입니다. 이 두 개념을 정확히 이해하고 활용하면, 우리가 필요한 자료를 효과적으로 해석하고 의사 결정을 쉽게 할 수 있을 것입니다.